어린 왕자
| 2 초 | 128 MB | 42131 | 19077 | 16072 | 46.264% |
문제
어린 왕자는 소혹성 B-664에서 자신이 사랑하는 한 송이 장미를 위해 살아간다. 어느 날 장미가 위험에 빠지게 된 것을 알게 된 어린 왕자는, 장미를 구하기 위해 은하수를 따라 긴 여행을 하기 시작했다. 하지만 어린 왕자의 우주선은 그렇게 좋지 않아서 행성계 간의 이동을 최대한 피해서 여행해야 한다. 아래의 그림은 어린 왕자가 펼쳐본 은하수 지도의 일부이다.
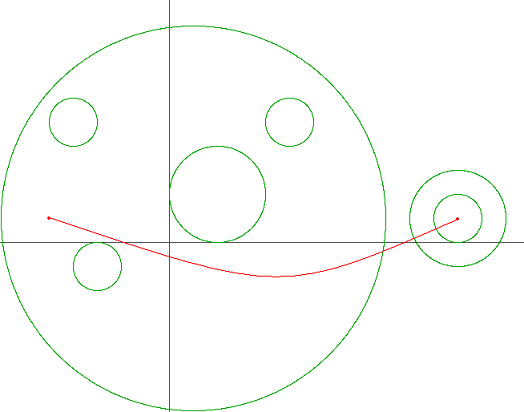
빨간 실선은 어린 왕자가 출발점에서 도착점까지 도달하는데 있어서 필요한 행성계 진입/이탈 횟수를 최소화하는 경로이며, 원은 행성계의 경계를 의미한다. 이러한 경로는 여러 개 존재할 수 있지만 적어도 3번의 행성계 진입/이탈이 필요하다는 것을 알 수 있다.
위와 같은 은하수 지도, 출발점, 도착점이 주어졌을 때 어린 왕자에게 필요한 최소의 행성계 진입/이탈 횟수를 구하는 프로그램을 작성해 보자. 행성계의 경계가 맞닿거나 서로 교차하는 경우는 없다. 또한, 출발점이나 도착점이 행성계 경계에 걸쳐진 경우 역시 입력으로 주어지지 않는다.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주어지며, 세 번째 줄부터 n줄에 걸쳐 행성계의 중점과 반지름 (cx, cy, r)이 주어진다.
출력
각 테스트 케이스에 대해 어린 왕자가 거쳐야 할 최소의 행성계 진입/이탈 횟수를 출력한다.
제한
- -1000 ≤ x1, y1, x2, y2, cx, cy ≤ 1000
- 1 ≤ r ≤ 1000
- 1 ≤ n ≤ 50
- 좌표와 반지름은 모두 정수
예제 입력 1 복사
2
-5 1 12 1
7
1 1 8
-3 -1 1
2 2 2
5 5 1
-4 5 1
12 1 1
12 1 2
-5 1 5 1
1
0 0 2
예제 출력 1 복사
3
0
예제 입력 2 복사
3
-5 1 5 1
3
0 0 2
-6 1 2
6 2 2
2 3 13 2
8
-3 -1 1
2 2 3
2 3 1
0 1 7
-4 5 1
12 1 1
12 1 2
12 1 3
102 16 19 -108
12
-107 175 135
-38 -115 42
140 23 70
148 -2 39
-198 -49 89
172 -151 39
-179 -52 43
148 42 150
176 0 10
153 68 120
-56 109 16
-187 -174 8
예제 출력 2 복사
2
5
3
오~ 1004번~ 어린왕자 갬성~
문제 읽으면서 한 송이 장미... 장미야.... 눈물 주륵......
하다가 지도 보고 빠른 기절. 눈물 다 들어감
이게 뭐지?
진짜 그래프를 보고 모든 정신이 사라질 것 같다.. 그래도 장미를 구해야 하니까 정신을 붙잡고 지도 말고 글이라도 읽어보기라도 하자.
적어도 3번의 행성계 진입/이탈... 그래프를 보면 원 세 개를 진입/이탈하는 것 같긴 하다. 원을 최대한 피해 가라는 거잖어.. 근데 이걸 어떻게 구현하라는 거야...
지도로 화면에 띄워서 그냥 세보면 안 되는 거니?
어? 지도도 있는 것 같은데 말이야 어린 왕자야... 근데 어린왕자 이름이 뭐였지 검색해봐야겠다
검색 완료. 이름이 작중에 안 나온단다.. 글고 얘 별 이름은 소행성 B612였음 그니까 이 문제의 어린 왕자는 '그' 어린 왕자가 아니라 짭 어린 왕자였다. 속았다. 그러니까 이런 감성 없는 지도를 갖고 다니지 떼잉쯧
입력 테스트 케이스 개수 T
출발점 도착점
행성계 개수 n
행성계 중점 반지름
...
걍 뭐 어떡해야 할 지를 모르겠다 사실 이거 쓰기 시작한 지가 벌써 7월 8일 00시... 지금은 7월 9일 23시 6분....
회피하다가 다시 앉았는데 어떻게 해야 하는 거야...
그래
입력을 어떻게 받을 건지부터 생각해보자..............
?출발점 도착점을 뭐 어떻게 받아야 하는 거임. 그냥 int형으로 받으면 되나?
일단 입력 포기하고 어떻게 풀면 좋을 지 생각해보자.
초등학교 때 배웠던 원의 정의를 떠올려보자^^... 한 점에서 같은 거리로 떨어진 점의 모임이었나 암튼 이거였는데 이걸 아직도 기억하는 이유는 파릇파릇한 유망주갓기였던 시절.... 이거 한 문제를 틀려서 올백을 놓쳤기 때문이다. ㅎ 진짜 개억울햇고 그 당시 나의 라이벌은 올백을 맞아서 그 당시 굉장히 분해했던 기억이 있다. 어쩌면... 울었나?!
암튼 간에 원의 중점하고 반지름 있으면 넓이도 구할 수 있고 둘레도 구할 수 있잖아... 이건 뭐가 필요한 거야... 일단 둘레로 진입하는 순간이 중요한 것 같기도 하고 넓이 안으로 들어오는 게 중요한 것 같기도 하고 근데 쓰다 보니까 원에서 빠져나가는 순간 ... 이걸 뭐라고 해야 하지 안밖이 중요한 것 같기도 함 들어가고 나가는 순간...
그러면 입력을 어떻게 받아야 하냐고.....! 이걸 다 배열로 받아?
그래..... 일단 저 그림에 있는 잉여4총사.. 이런 원은 받아도 걍 버리면 되는데....

오 너무 하기 싫어서 미루다보니까 11일 밤 됨 그 사이에 장미 죽었을 듯;;
저 개발새발 글씨는 뭐지?
장미님... 장미님은 아직 안 죽었네요~~????? 예.. 구하러 갈게요....
저 잉여 4개의 원은 굳이 신경 안 써도 된다는 게... 어.... 흠...... 그 출발점과 도착점이 저 원에 안 들어가 있으면 저 원은 버려도 되는 거 아닌가.... 핳하하 하하하하하하하하하기싫다
이클립스 켜지는 동안 잠깐 누워있겠다는 게 벌써 두 시간이 지났다.
이제 47분 남음..
cx cy에서 반지름 +- 안에 들어있으면 카운트 하면 되겠지... 예를 들면 cx cy가 3, 2고 반지름이 1일 때 원은 2~4 1~3에 . 되니까?? 대신 둘 다 같은 원에 있으면 더하면 안 되겠지요....???
그렇게 얼렁뚱땅 완성된 첫 번째 코드..
import java.util.Scanner;
public class BJ_1004 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt(); // 테스트 케이스 개수 T
for (int i = 0; i < T; i++) {
int x1 = sc.nextInt(); // 출발점 x
int y1 = sc.nextInt(); // 출발점 y
int x2 = sc.nextInt(); // 도착점 x
int y2 = sc.nextInt(); // 도착점 y
int count = 0; // 행성계 진입/이탈 횟수 담을 변수
int n = sc.nextInt(); // 행성계 개수
for (int j = 0; j < n; j++) {
int cx = sc.nextInt(); // 행성계 중점 x
int cy = sc.nextInt(); // 행성계 중점 y
int r = sc.nextInt(); // 행성계 반지름
if (cx - r < x1 && cx + r > x1 && cy - r < y1 && cy + r > y1) {
if (cx - r < x2 && cx + r > x2 && cy - r < y2 && cy + r > y2) {
continue;
}
count++;
}
else if (cx - r < x2 && cx + r > x2 && cy - r < y2 && cy + r > y2) {
count++;
}
}
System.out.println(count);
}
sc.close();
}
}
예상했겠지만 역시나^^

안타깝지만 장미를 구하지 못했다.
장미야 미안
지금 문제점을 찾았다. 앞에서는 실컷 원의 정의 어쩌고 하더니 너무 단순하게 직사각형처럼 다루고 있었다... 빡대갈?;;
수정한 두 번째 코드!!!
import java.util.Scanner;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt(); // 테스트 케이스 개수 T
for (int i = 0; i < T; i++) {
int x1 = sc.nextInt(); // 출발점 x
int y1 = sc.nextInt(); // 출발점 y
int x2 = sc.nextInt(); // 도착점 x
int y2 = sc.nextInt(); // 도착점 y
int count = 0; // 행성계 진입/이탈 횟수 담을 변수
int n = sc.nextInt(); // 행성계 개수
for (int j = 0; j < n; j++) {
int cx = sc.nextInt(); // 행성계 중점 x
int cy = sc.nextInt(); // 행성계 중점 y
int r = sc.nextInt(); // 행성계 반지름
boolean startInside = isInside(x1, y1, cx, cy, r); // 시작점이 원 안에 있는지
boolean endInside = isInside(x2, y2, cx, cy, r); // 도착점이 원 안에 있는지
if (startInside != endInside) {
count++;
} // 하나만 원 안에 있을 때 카운트 횟수 더해주기
}
System.out.println(count);
}
sc.close();
}
// 원 내부에 있는지 확인해서 true false로 반환
static boolean isInside(int x, int y, int cx, int cy, int r) {
return (x - cx) * (x - cx) + (y - cy) * (y - cy) < r * r;
}
}
판단하는 부분을 메소드로 빼버리고 코드 내부에서 if 문으로 하느니 boolean 타입으로 반환 받아서 둘 중에 하나만 true일 때 더해주는 걸로 바꿨다.
둘 다 true일 때 -> 같은 원 안에 있으니까 통과할 필요 없음. 둘 다 false 일 때 -> 저 위에 잉여원임
둘 중 하나만 안에 있을 때 더해주면 된다.
결과는

휴 장미야
아주 무겁고 느리지만 너를 구할 수 있었어... 다행
'백준 풀기' 카테고리의 다른 글
| 백준 3273번: 두 수의 합 with Java (0) | 2024.07.13 |
|---|---|
| 백준 15655번: N과 M (6) with Java (0) | 2024.07.12 |
| 백준 2559번: 수열 with Java (0) | 2024.07.07 |
| 백준 15657번: N과 M(8) with Java (1) | 2024.07.05 |
| 백준 9375번: 패션왕 신해빈 with Java (0) | 2024.07.04 |